di roberto vacca, 20 marzo 2020
Le malattie infettive si diffondono dapprima lentamente. Quando il numero dei contagiati cresce, accelera sempre più fino a sembrare esponenziale – ma poi comincia a decrescere il numero dei contagiabili. La pendenza delle curve del numero totale dei contagiati e di quello dei morti, che cresceva gradualmente, diminuisce fino ad annullarsi: il numero raggiunge un valore massimo costante A, detto asintoto. Non muore più nessuno: l’epidemia è finita. È più significativo considerare il numero dei decessi [supponendo che i certificati di morte siano giusti]: infatti i numeri dei contagi dipendono da quanti tamponi si fanno.
Trovò le equazioni che descrivono questi processi, nel 1930, il fisico Vito Volterra [1]. Queste definiscono le curve logistiche a S – il diagramma seguente rappresenta i decessi da corona virus in Cina.
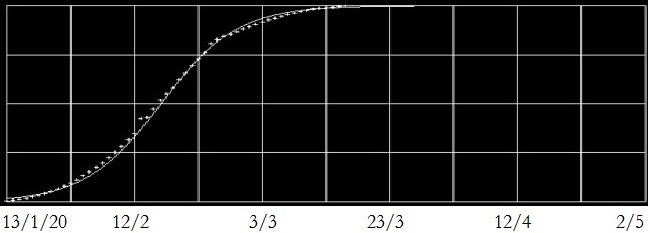Cina – Morti cumulative x da COVID-19 dal 13 Gennaio al 16 Marzo 2020 – Asintoto A = 3215 – ordinata del lato superiore orizzontale del rettangolo. La curva a tratto continuo è data dall’equazione x = 3215/(1 + e(16,847 t – 29,382))
Fonte dati: OMS Organizzazione Mondiale della Sanità
L’epidemia in Italia è cominciata un mese e mezzo più tardi che in Cina. Come mostra il grafico a pagina seguente, la crescita è stata molto più rapida: il numero dei morti ha superato quello cinese. Sembrerebbe avviato a fermarsi fra breve raggiungendo un asintoto inferiore a 10.000 (mentre taluno sta avanzando previsioni molto più catastrofiche), ma è certo consigliabile seguire prescrizioni prudenti e osservare il decorso.
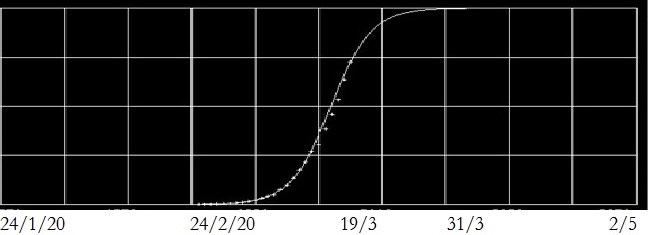
Italia – Morti cumulative x da COVID-19 dal 24 Febbraio al 19 Marzo 2020
Asintoto A = 4690 – ordinata del lato superiore orizzontale del rettangolo
L’equazione che presenta il migliore fit è: x = 4690/(1 + e(31.5 t – 63,6))
L’asintoto è di 4690. I morti al 19 Marzo erano 3405
Fonte dati: Ministero della Salute
Il COVID-19, come gli altri virus influenzali, sembra soggetto a essere eliminato dalle alte temperature. Lo ha dimostrato in una serie di esperimenti Jungyuan Wang dell’Università Beihang (Beijing).
Le regole imposte per limitare i contatti umani sono razionali (come dimostra l’esperienza di Vo Euganeo). Non furono adottate durante l’epidemia di influenza “asiatica” del 1957 che provocò 30.000 morti in Italia, 116.000 negli Stati Uniti e oltre un milione nel mondo.
[1] Detto x il numero di malati o dei morti e A il numero totale dei contagiabili – o dei morti – l’equazione differenziale di Volterra dice che la derivata di x rispetto al tempo è uguale al prodotto x (A – x) moltiplicato per una costante K. Cioè: dx/dt = K x (A-x) la cui soluzione è x = A/(1 + e(Bt+C)). A e K non sono noti, ma A, B e C si possono determinare con procedure empiriche in base ai valori registrati di x.
*Roberto Vacca (Roma, 31 maggio 1927) è un ingegnere, matematico, divulgatore scientifico, scrittore e accademico italiano. Tra le sue moltissime opere: Il medioevo prossimo venturo, 1971; Manuale per un’improbabile salvezza, 1974; La via della ragione, 1993; Salvare il prossimo decennio, 2011; Come fermare il tempo e riempirlo di buone idee, Mondadori, 2016.
